
Από τον Γιάννη Μπρούζο*
*Το κείμενο αυτό είναι αφιερωμένο στα παιδιά που μέσα στις διακοπές του Πάσχα για άλλη μια φορά έχουν φορτωθεί το σταυρό της προετοιμασίας για εξετάσεις και βαθμούς, στα παιδιά που το σχολείο ποτέ δεν θα τους μάθει -με το καταναγκαστικό αναλυτικό του πρόγραμμα- πως υπάρχουν παράλογοι και φανταστικοί αριθμοί, πως κανείς δεν είναι τέλειος και πλήρης ούτε καν τα μαθηματικά, και στον πατέρα μου για όσα μου έμαθε.*
Όταν ο πατέρας μου μας μιλούσε για τα μαθηματικά, ξεκινούσε πάντα -και ανεξαρτήτως ηλικίας μας ή θέματος που ειχε να διδάξει- από τα (απειρο)σύνολα των αριθμών. Από τις ανάγκες των ανθρώπων και την φαντασία των μαθηματικών ξεπηδούσαν αριθμοί με περίεργα ονόματα: φυσικοί, ακέραιοι, ρητοί, άρρητοι, πραγματικοί, φανταστικοί, μιγαδικοί! Ήταν μια συναρπαστική ιστορία των μαθηματικών και ταυτόχρονα ιστορία της ανθρώπινης σκέψης και δράσης.
Σαν καλός του μαθητής λέω και εγώ περίπου την ίδια ιστορία στα παιδιά που διδάσκω και εδώ θα την διηγηθώ και εσάς. Αφορμή είναι ένας πρόσφατος διάλογος με μια μαθήτριά μου:
-Την Παρασκευή παίρνουμε βαθμούς και δεν μου αρέσουν οι βαθμοί.
-Τί εννοείς δεν σου αρέσουν;
-Να, οι βαθμοί είναι σαν τα λεφτά. Είναι αριθμοί που μετράνε.
Με συγκλόνησε αμέσως η φοβερή αυτή σκέψη που έκρυβε τόσα πολλά και βαθιά πράγματα μέσα της. Πρώτα απ όλα, η παρομοίωση -η εξίσωση θα λέγαμε- των βαθμών με τα λεφτά. Συνειδητοποίησα ότι είναι τα δύο πιο άμεσα ζητημάτα με τα οποία τα παιδιά έρχονται δυστυχώς σε πρώτη επαφή με τα μαθηματικά, και που οι περισσότεροι συνεχίζουν και ως ενήλικες να πιστεύουν οτι είναι η μεγαλύτερη αξία των μαθηματικών. Για αυτό και συνήθως τα μισούν.
Μετά με στοίχειωσε η απίστευτη φράση
“Είναι αριθμοί που μετράνε”.
Βεβαίως το ρήμα “μετράω” έχει διττή έννοια: “υπολογίζω, προσδιορίζω το μέγεθος” και “θεωρούμαι αξιος, σημαντικός”. Τόμοι ολόκληροι φιλοσοφίας θα μπορούσαν να γραφτούν πάνω σε αυτό και μαλιστα οταν υποκείμενο της πρότασης δεν είμαστε εμείς οι άνθρωποι που μετράμε, αλλά οι ίδιοι οι αριθμοί!
Και ακόμα πιο εξωφρενικό: Αν υπάρχουν αριθμοί που μετράνε, υπάρχουν και αριθμοί που ΔΕΝ μετράνε; Έχω πει εγώ κάτι τέτοιο στο παιδί και του μπαίνουν αυτές οι ιδέες; Ε λοιπόν ίσως ναι….
Αν έχετε κουραστεί να ακούτε τα “δεν βγαίνουν τα νούμερα”, τα “αξιολόγηση των επιδόσεων της οικονομίας και των αριθμών”, τα “που θα βρειτε τα λεφτά” και τα “λεφτά υπάρχουν”, συνεχίστε να διαβάζετε αυτό το κείμενο γιατί πιστεύω βαθιά οτι η ενασχόληση με τους αριθμούς και τα μαθηματικά δεν είναι μια καταβύθιση σε όλα αυτά τα θλιβερά, αλλά αντίθετα μια απόδραση απο όλα αυτά.
Μια απόδραση απο τους “αριθμούς που μετράνε”, από τους αριθμούς που αξίζουν πιο πολύ απο τις ζωές των ανθρώπων. Μια απόδραση στον κόσμο που οι αριθμοί έχουν ζωή και η αξία μιας ζωής, μιας σκέψης, ενός αισθήματος, ενός ήχου, ενός χρώματος, ενός αριθμού είναι τόσο άπειρη που κανένας αριθμός από αυτούς που “μετράνε” δεν μπορεί να την μετρήσει. Ας αρχίσουμε λοιπόν την εκδρομή μας στον κόσμο των αριθμών.
Οι πρώτοι φυσικοί αριθμοί: τα άτομα των μαθηματικών
Και ένα μωρό όταν ξεκινάει σιγά σιγά να ψαχουλεύει τον κόσμο γύρω του, αρχίζει και καταλαβαίνει ότι υπάρχουν ίδια πράγματα, ή πράγματα παρόμοια που μπορώ να τα βάλω σε ένα σακουλάκι, ένα “σύνολο” και να πω ότι έχω “τόσα” τέτοια. Ένα μπαλάκι μπορεί να γίνει δυο μπαλάκια, 3 μπαλάκια … -κι ας είναι διάφορα χρώματα, δεν μας ενδιαφέρει αυτό, αργότερα μπορούμε να χωρίσουμε και κατά χρώματα και κατά μεγέθη κλπ-. Έτσι έρχονται φυσικά στη ζωή μας οι “φυσικοί” αριθμοί, τα 1,2,3,4…. και τελειωμό δεν έχουν.
Το βρέφος γρήγορα καταλαβαίνει βέβαια ότι υπάρχουν και άλλα γύρω μας όπως η μαμά και ο μπαμπάς που είναι μοναδικοί. Έτσι και μέσα στους φυσικούς αριθμούς υπάρχουν κάποιοι μοναδικοί αριθμοί οι “πρώτοι αριθμοί”. Αν προσπαθήσει ένα μωρό, ένα παιδί, ή ένας ενήλικας να χωρίσει ας πούμε τον αριθμό 7 στα 2 στα 3, στα 4 κλπ δεν θα τα καταφέρει ποτέ, πάντα κάτι θα περισσεύει. Οι αριθμοί λοιπόν που χωρίζονται ακριβώς (διαιρούνται) μόνο στον εαυτό τους και στη μονάδα (δηλαδή δεν χωρίζονται πρακτικά) είναι οι πρώτοι αριθμοί.
Τώρα όσο αθώοι και να φαίνονται, οι πρώτοι αριθμοί είναι σαν τα άτομα της φυσικής. Ενώσεις (ή καλύτερα πολλαπλασιασμοί) αυτών των ατόμων μπορούν να φτιάξουν όλο τον κόσμο, δηλαδή όλους τους φυσικούς αριθμούς. Και αφού οι φυσικοί αριθμοί είναι άπειροι, είναι άπειροι και οι πρώτοι αριθμοί όπως μας δίδαξε ο Ευκλείδης.
Σκεφτείτε πόσο σημαντική είναι η σκέψη οτι ο πολύπλοκος κόσμος γύρω μας αποτελείται στην πραγματικότητα απο ενώσεις περιορισμένου αριθμού δομικών λίθων -των ατόμων-και πόσο σημαντικό είναι να τα ξέρουμε όλα αυτά τα τουβλάκια.
Και τα ξέρουμε: Είναι ο περιοδικός πίνακας των στοιχείων που μαθαίνουμε στη χημεία.
Και τώρα σκεφτείτε οτι στην πραγματικότητα όλοι σχεδον οι αριθμοί είναι ενώσεις απο τα τουβλάκια που είναι οι πρώτοι αριθμοί και πόσο σημαντικό είναι να τους ξερουμε.
Ε, λοιπόν ετοιμαστείτε για την βόμβα: ΔΕΝ τους ξέρουμε ακόμα καλά.
Ναι ακριβώς εκεί στην καρδιά των μαθηματικών στην θεωρία των αριθμών υπάρχει ακόμα ένα μεγάλο μυστήριο, που όποιος το λύσει θα μας ταξιδέψει σε έναν κόσμο που δεν έχουμε καν ακόμα φανταστεί, όπως εκείνοι που μας εξήγησαν τα άτομα της φυσικής.
Το πρόβλημα με τους πρώτους αριθμούς είναι ότι δεν μπορείς να ξέρεις πότε θα ξεπροβάλλουν καθώς πηγαίνεις προς το άπειρο. Ας πούμε ότι έχεις βρει έναν πρώτο αριθμό πχ το 17, πότε θα εμφανιστεί ο επόμενος;
Οι μεγαλύτεροι μαθηματικοί ασχολήθηκαν με αυτό το πρόβλημα και που κατέληξαν; Σε μια υπόθεση -μια εικασία θα λέγαμε- την Υπόθεση Ρίμαν.
Δηλαδή σε κανένα σίγουρο αποδεδειγμένο συμπέρασμα, αλλά μια μεγαλειώδη υπόθεση η οποία λειτουργεί εξωφρενικά καλά, και για αυτό πασχίζουν οι μαθηματικοί πάνω απο 150 χρόνια να την αποδείξουν.
Εκείνη όμως αντιστέκεται, δεν ξέρουμε για πόσο καιρό, ίσως για μια βδομάδα, ίσως για έναν αιώνα, ίσως μια αιωνιότητα.
Γιατί ενδέχεται, όπως μας έμαθε ένας γίγαντας των μαθηματικών της λογικής ο Γκέντελ, η υπόθεση Ρίμαν να μην είναι καν αποδείξιμη στο πλαίσιο των υπαρχόντων αξιωμάτων. Δηλαδή να χρειαστούμε να επεκτείνουμε τα μαθηματικά που είναι πάντα “μη πλήρη” για να την αποδείξουμε.
Fail και “μη πλήρη” μαθηματικά; Ναι, γιατί κανείς δεν είναι τέλειος ούτε καν τα μαθηματικά, και αυτό είναι ένα μεγάλο μάθημα για να μην παίρνουμε τους βαθμούς, τους “αριθμούς που μετράνε” το τέλειο τόσο σοβαρά.
Για να μιλήσουμε όμως για την Υπόθεση Ρίμαν και τους πρώτους αριθμούς πρέπει να μιλήσουμε πρώτα για τους πιο περίπλοκους αριθμούς τους φανταστικούς και τους μιγαδικούς. Στο ταξίδι των μαθηματικών ένα εμπόδιο, ένα πρόβλημα είναι πάντα για καλό γιατί μας οδηγεί στο να ανακαλύψουμε όλο και πιο περίεργα και όμορφα μαθηματικά για να το ξεπεράσουμε.
Αν μπορείς να το φανταστείς, υπάρχει
Οι επαναστάσεις στην ιστορία των μαθηματικών βασίζονταν πάντα στην δημιουργικότητα, την φαντασία και την τόλμη των ανθρώπων που προσπαθούσαν να επιλύσουν συγκεκριμένα προβλήματα. Οι άνθρωποι που πήγαιναν “by the book” που απλά προσαρμοζόντουσαν σε αυτά που τους επιβάλλονταν το μόνο που κατάφερναν είναι να πάνε πίσω τη ζωή (προσωρινά).
Τα προβλήματα στα μαθηματικά παίρνουν πολλές φορές την μορφή εξισώσεων. Οι εξισώσεις δεν είναι τίποτα άλλο παρα καθημερινά προβλήματα που αναζητούν μια λύση εκφρασμένα με τα σύμβολα των μαθηματικών. Και οι άνθρωποι έμαθαν πολύ νωρίς να λύνουν τέτοια προβλήματα χρησιμοποιώντας τους φυσικούς αριθμούς και τις πράξεις μεταξύ τους. Δηλαδή προσθέσεις αφαιρέσεις πολλαπλασιασμούς και διαιρέσεις.
Ιδιαίτερα οι διαιρέσεις έδωσαν όνομα σε νέους αριθμούς τα κλάσματα ή αλλιώς τους “ρητούς αριθμούς”. Οι ρητοί αριθμοί “οι λόγοι” που θα έλεγαν οι αρχαίοι Έλληνες, είναι μια πολλή μεγάλη ομάδα αριθμών, όλων των αριθμών που μπορούν να γραφτούν υπό μορφή ενός κλάσματος δηλαδή μιας διαίρεσης φυσικών αριθμών. Και για αυτό είναι αριθμοί που μπορούν να “ειπωθούν” δηλαδή ρητοί. Ακόμα και οι μεγάλοι δεκαδικοί αριθμοί είναι ρητοί: πχ ο 7.6538=76538/10000.
Πάνω από 200 χρόνια π.Χ. οι Κινέζοι στο φοβερό βιβλίο “Εννιά Κεφάλαια Μαθηματικής Τέχνης” εισήγαγαν τους αρνητικούς αριθμούς. Οι αρνητικοί αριθμοί βασίζονται στην ιδέα ότι κάθε πράγμα έχει και το αντίθετό του που είναι εξίσου υπαρκτό με αυτό. Έτσι και οι αριθμοί, έχουν τους θετικούς και τους αρνητικούς. Οι λαοί της ανατολής, Κινέζοι, Ινδοί, Άραβες, ήταν πολύ πιο ανοιχτοί στην διαλεκτική των αντιθέσεων και έτσι αποδέχτηκαν και ανέπτυξαν πολύ αυτή την ιδέα. Αντίθετα στην Ευρώπη τους αποδεχτήκαμε μόλις τον 17ο αιώνα μ.Χ…
Στους αρχαίους έλληνες άρεσε να ξεκινούν απο αξιώματα, κάποιες δηλαδή διαισθητικά λογικές προτάσεις, και να συνάγουν συμπεράσματα, θεωρήματα και άλλες αποδεδειγμένες προτάσεις. Οι κινέζοι απο την άλλη όπως και οι άραβες έψαχναν για τις πιο γενικές λύσεις σε προβλήματα. Έτσι οι αρνητικοί αριθμού μπορουν να μας λύσουν πχ την εξίσωση-προβλημα x+3=1 (x=-2). Οι αρνητικοί αριθμοί μαζί με τους θετικούς φυσικούς αποτελούν το σύνολο των ακέραιων αριθμών.
Πίσω στην αρχαία Ελλάδα τα πράγματα ήταν σχετικά ήρεμα με τους φυσικούς και τους ρητούς, και έδιναν στους θαυμαστές του “Λόγου” την αίσθηση της αρμονίας του κόσμου. Ώσπου ένας μαθητής του Πυθαγόρα ο Ίππασος, τόλμησε να κάνει την εξής απλή σκέψη: Αν έχω ένα ορθογώνιο τρίγωνο που και οι δυο κάθετες πλευρές του έχουν μήκος 1 πόσο είναι το μήκος της υποτείνουσας; Σύμφωνα με το πυθαγόρειο θεώρημα -που πρώτος ο Πυθαγόρας απέδειξε αν και βέβαια είχαν προηγηθεί μεσοποτάμιοι λαοί στην διατύπωση του- έχουμε: ![]()
Άρα πόσο είναι το x σε αυτή την δευτεροβάθμια εξίσωση (όπου το x είναι στο τετράγωνο); Και έτσι ήρθε ένας νέος αριθμός ο ρίζα √2. Αυτός ο αριθμός όμως είχε ένα μεγάλο πρόβλημα που χάλαγε όλο το αρμονικό κοσμοείδωλο των Πυθαγορείων. Δεν μπορούσε να γραφτεί ως κλάσμα, δεν ήταν δηλαδή ρητός, είχε άπειρα δεκαδικά ψηφία χωρίς καμιά επανάληψη όλα ξεχωριστά. Δεν μπορούσες δηλαδή με τίποτα να τον γράψεις, να τον διαβάσεις, να τον πεις, να τον ονομάσεις. Ο Πυθαγόρας, παρόλο που ήταν ο ίδιος και η εξίσωσή του υπεύθυνη για την ύπαρξη αυτού του αριθμού, θύμωσε τρομερά με αυτόν τον ξένο, τον “άρρητο αριθμό”, και έβαλε την συμμορία του να πετάξουν τον Ίππασο στη θάλασσα.
Οι άρρητοι αριθμοί λοιπόν μια ιστορία επαναστατική. Στα αγγλικά που οι ρητοί αριθμοί ονομάζονται rational, δηλαδή αριθμοί του “Λόγου”, οι άρρητοι αριθμοί ονομάστηκαν irrational, δηλαδή οι αριθμού του “παραλόγου”.
Οι παράλογοι λοιπόν αυτοί αριθμοί όχι μόνο υπάρχουν αλλά είναι και αμέτρητα άπειροι σε αντίθεση με τους ρητούς που όπως απέδειξε ο Κάντορ είναι μετρήσιμα άπειροι.
Δηλαδή υπάρχουν και διαφορετικά “άπειρα”? Ναι, όχι μόνο υπάρχουν αλλά ο ανθρώπινος μαθηματικός νους τα έχει κατατάξει -αφου ψιλοτρελάθηκε βέβαια.
Ακόμα πιο επαναστατική η ιστορία των αριθμών που ήρθαν ως λύση ενός άλλου προβλήματος στις δευτεροβάθμιες εξισώσεις: τί γίνεται αν η εξίσωση καταλήγει στο ![]() ; Δυστυχώς κανένας από τους πραγματικούς αριθμούς -όπως ονομάζονται οι ρητοί και οι άρρητοι μαζί- δεν μπορείς να τον πολλαπλασιάσεις με τον εαυτό του και να σου βγάλει αρνητικό αριθμό.
; Δυστυχώς κανένας από τους πραγματικούς αριθμούς -όπως ονομάζονται οι ρητοί και οι άρρητοι μαζί- δεν μπορείς να τον πολλαπλασιάσεις με τον εαυτό του και να σου βγάλει αρνητικό αριθμό.
Ο τολμηρός Ιταλός μαθηματικός Bombelli όμως θα πει αφού μπορώ να τον φανταστώ υπάρχει θα τον ονομάσω με το πρώτο γράμμα της φαντασίας της λέξης imagination “i”.
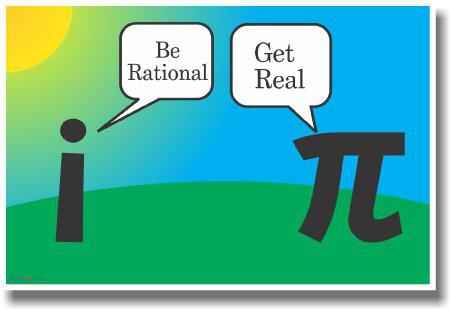
Και έτσι ήρθαν στον κόσμο μας οι φανταστικοί αριθμοί. Αυτοί είναι αριθμοί που πραγματικά δεν μετριούνται όχι με την έννοια ότι είναι άπειροι (που είναι) αλλά που δεν έχουν πραγματική υπόσταση σε ένα φυσικό πείραμα. Δεν μπορεί δηλαδή καμιά συσκευή να τους μετρήσει.
Όμως παρόλα αυτά οι φανταστικοί αριθμοί είναι απίστευτα χρήσιμοι στο να αναπαραστήσουμε (να φανταστούμε δηλαδή, να φτιάξουμε το image-την εικόνα, το imagination) φαινόμενα όπως τα κύματα που είναι σχεδόν όλη η φύση πέρα από τα σωματίδια. Κύμα είναι ο ήχος και η μουσική, το φως και τα χρώματα, ακόμα και τα στοιχειώδη σωματίδια, τα ηλεκτρόνια και όλα αυτά είναι σύμφωνα με την κβαντική φυσική και κύματα. Και τα κύματα αναπαρίστανται στα μαθηματικά με την βοήθεια των φανταστικών αριθμούς, των αριθμών της φαντασίας.
Τώρα επειδή στους μαθηματικούς αρέσουν οι μίξεις και οι προσμίξεις για να φτιάχνουν πιο σύνθετα και πιο όμορφα πράγματα, δημιούργησαν από το άθροισμα πραγματικών και φανταστικών αριθμών τους μιγαδικούς αριθμούς.
Εδώ κάπου τελειώνει η μέχρι τώρα κατασκευή αριθμών, αλλά θα σας φανεί ίσως απίστευτο, έπρεπε να φτάσουμε μέχρι και τους μιγαδικούς αριθμούς για να γυρίσουμε πίσω στους πρώτους -τα άτομα των αριθμών- και τα μεγάλα μυστήριά τους. Η εκδρομή μας στον αμέτρητα άπειρο κόσμο των αριθμών έκανε τον πρώτο της κύκλο.
Και ο κύκλος είναι ένα σχήμα δύο διαστάσεων μπορεί δηλαδή να αναπαρασταθεί και με φανταστικούς-μιγαδικούς αριθμούς, και έχει περίμετρο έναν άρρητο-παράλογο αριθμό το “π”.
Στην δεύτερη εκδρομή μας θα εστιάσουμε στον παράξενο κόσμο των πρωτων αριθμών.
Το ταξίδι στους “αριθμούς που δεν μετράνε” μόλις ξεκίνησε και τέλος δεν έχει.
*Ο Γιάννης Μπρούζος είναι διδάκτωρ Φυσικής
